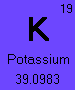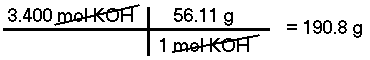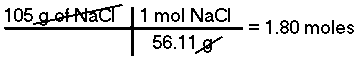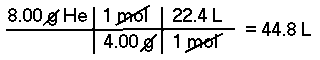What is the mole?
Understanding the concept of the mole is critical in chemistry. Without the idea of a mole, many of the fundamental elements of chemistry [no pun intended] cannot be understood.
The mole is the SI unit for the amount of a substance.
A mole is just a counting number, like "dozen", it is just certain number of particles.
If someone has a dozen eggs, that person has 12 eggs. Likewise, if someone has a mole of eggs, that person is said to have 6.022 x1023 eggs. This increadibly large amount is called Avogadro's number, named after the Italian scientist Amedeo Avogadro (pictured Left).
To get a sense of how large Avogadro's number is,
If one had a mole of pennies (6.022 x1023 pennies), one could give each person on Earth $926 billion dollars, and still have money left over.
- The formal definition of a mole is,
- "The mole is the amount of substance of a system which contains as many elementary entities as there are atoms in 0.012 kilogram of carbon 12."
There are 6.022142 x 1023 things in 1 mole of anything.
In Chemistry, moles are used to represent the number of atoms, molecules, ions, or formula units in a substance.
The official definition relies on the atomic mass of a Carbon-12 atom in order to obtain the number of particles in a mole. Since an atom has such a small mass, to simplify things, an atoms mass can be expressed in atomic mass units (amu). Each amu is about equal to the mass of a single proton or neutron in the nucleus of an atom or about 1.6605389 x10-24 grams. In the case of Carbon-12, a single atom has a mass of exactly 12 amu. In one mole of Carbon-12 atoms, the total mass of the combined particles would be exactly 12.00 grams.
Molar masses
Molar masses (sometimes called "molar weights") are very similar to the concept of atomic masses.
The molar mass of a substance is the mass of 1 mole of that substance.
The molar mass of a pure element is equal to its atomic mass (usually given in units of grams).
The atomic mass of an element is equal to the number of protons plus the number of neutrons in the atom's nucleus (electrons have a negligible mass). However, quite often, an atom from one element can have a different number of neutrons in its nucleus than another atom of the same element, when this is the case, the element is said to have more than one isotope. In the case of atoms with more than one isotope, the atomic weight shown on the periodic table and the value used in calculations is the average atomic mass. The average atomic mass is a weighted average of the elements isotopes based on their percent natural abundance.
For example:
The element Potassium (#19) has 3 naturally occurring isotopes, Potassium-39, Potassium-40, and Potassium-41.
The percent abundance of each of Potassium's isotopes are listed below:
Isotope |
Atomic Mass (ma/u) |
% Abundance |
39K |
38.9637074 |
93.2581 % |
40K |
39.9639992 |
0.0117 % |
41K |
40.9618254 |
6.7302 % |
To calculate the average atomic mass of Potassium, add the products of the each isotope's atomic mass multiplied by its percent abundance.
(38.9637074 * .932581) + (39.9639992 * .000117) + (40.9618254 * .067302)
= 39.0983 g/molNotice that the average atomic mass calculated equals the number shown on the periodic table.
The molar mass of an ionic compound or molecule is the mass of 1 mole of that substance. The molar mass of a substance is simply the sum of the molar masses of each atom in the chemical compound.
For example:
The chemical formula of water is H2O, meaning that it has 2 Hydrogen atoms and 1 Oxygen atom in each water molecule, meaning that in 1 mole of water, there are two 2 moles of Hydrogen atoms and 1 mole of Oxygen atoms. To find the molar mass of this substance, add each of the molar masses of the elements in water in their correct proportions.The molar mass of Hydrogen is 1.0079 g/mol
The molar mass of Oxygen is 15.9994 g/mol
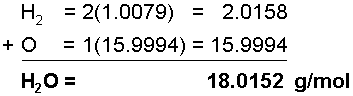
It is common when expressing molar masses to round off to the first two decimal places, making the molar mass of water 18.02 g/mol.
When determining molar masses, the mass of the electrons around an atom are considered negligible and are ignored for calculation purposes.
Mole conversions
It is often useful to be able to convert between mass and the number of moles of a particular substance, this can be done using the molar mass. Remember the units of molar mass are grams per mole (g/mol), meaning that 1 mole of any substance has a fixed mass.
To convert from moles of a substance to grams, multiply the number of moles by the molar mass.
For example:
What is the mass of 3.400 moles of Potassium Hydroxide (KOH)?The molar mass of KOH is calculated to be 56.11 g/mol, therefore, there are 190.8 grams in 3.400 moles.
To convert from grams of a known substance to number of moles, divide the substance's mass by its molar mass.
For example:
How many moles are there in 105 grams of Sodium Chloride (NaCl)?The mass of 1 mole of NaCl is 58.44 g/mol, therefore, there are 1.80 moles of Sodium Chloride in 105 grams of NaCl.
There is one other important mole conversion, converting between the number of moles and the volume of an ideal gas. Although there is no such thing as a perfectly ideal gas in real life, the ideal gas law can be used to approximate the relationship between the number of moles of a gas and its volume (V), pressure (P) and temperature (T).
The gas rate constant (R) can have a value of 8.2054 x10-2 L atm mol-1 K-1
At STP, 1 mole of an ideal gas has a volume of 22.4 Liters.
To convert from moles of an ideal to Liters at STP, multiply the number of moles by 22.4.
For example:
Approximately, what is the volume at STP of 8.00 grams of Helium (He)?This is a two part problem; first one must convert grams of Helium to moles of Helium and then convert moles to Liters of Helium.
The molar mass of Helium is 4.00 g/mol, therefore, there are 2.00 moles of Helium in 8.00 grams. At STP, 1 mole of an ideal gas has a volume of 22.4 Liters, therefore 2.00 moles of Helium has a volume of about 44.8 Liters.
Last updated: 02/25/2006