Measurement
In science, as in everyday life, it is important to be able to communicate information clearly so others will be able to understand you. It is necessary to have a standard on which to base measurements on. To do this, many different measurement systems have been developed and adopted over time, each with its own system of units. With so many different measurement systems in use, it is difficult to express quantities in a way which everyone will be able to understand, hence the need for a common standard of measurement which everyone can be familiar with.
The metric system was first developed in France during the late 1700s as a logical system of measurement based on well defined units and over time, the metric system has become widely accepted throughout the world. The United States has made an effort to moving toward the metric system by redefining its Imperial units in terms of metric units and by passing the Metric Conversion in 1975 to promote the use of the metric system in the United States, yet most people still tend to use the old system.
The International System of Units (SI system)
The SI system (short for the French name Système International d'Unités, or International System of Units) is largely based off of the metric system, sharing many common units. Developed in 1960, the SI system has become the accepted system of measurement for use in many applications, most notably, science.
The SI system has seven basic units, from which all other units can be derived.
| Quantity | Unit Name | Symbol |
| Mass | kilogram | kg |
| Length | meter | m |
| Time | second | s |
| Electrical Current | ampere | A |
| Temperature | kelvin | K |
| Amount of a Substance | mole | mol |
| Luminous intensity | candela | cd |
Unit Definitions
Currently, each of the base units are defined as follows,
- kilogram*
- The kilogram is the unit of mass; it is equal to the mass of the international prototype of the kilogram.*As of May 20, 2019, this is no longer true due to the redefinition of the kilogram, and other units, based on fundemental physical laws.
- meter
- The length of the path traveled by light in vacuum during a time interval of
1/299 792 458 of a second. - second
- The second is the duration of
9,192,631,770 periods of the radiation corresponding to the transition between the two hyperfine levels of the ground state of the cesium 133 atom. - ampere
- The ampere is that constant current which, if maintained in two straight parallel conductors of infinite length, of negligible circular cross-section, and placed 1 meter apart in vacuum, would produce between these conductors a force equal to
2 x 10-7 newton per meter of length. - kelvin
- The kelvin, unit of thermodynamic temperature, is the fraction 1/273.16 of the thermodynamic temperature of the triple point of water.
- mole
- 1. The mole is the amount of substance of a system which contains as many elementary entities as there are atoms in 0.012 kilogram of carbon 12; its symbol is "mol."
2. When the mole is used, the elementary entities must be specified and may be atoms, molecules, ions, electrons, other particles, or specified groups of such particles. - candela
- The candela is the luminous intensity, in a given direction, of a source that emits monochromatic radiation of frequency
540 x 1012 hertz and that has a radiant intensity in that direction of 1/683 watt per steradian.
* The kilogram is the only unit still defined by a physical object, as opposed to physical constants. The original Platinum-Iridium cylinder used as the standard for the kilogram is kept under glass at the BIPM (Bureau International des Poids et Mesures) in France and is periodically checked against other nations' standards to ensure the highest possible accuracy.*As of May 20, 2019, this is no longer true due to the redefinition of the kilogram, and other units, based on fundemental physical laws.
Unit Prefixes
One of the nicest features of the metric/SI system is that the units are based on powers of ten, meaning that the there is a very simple conversion between large and small units based on a common base. By contrast, the Imperial system has very little relationship between the large and small units of a given quantity.
A prefix can be added to the unit to act as a multiplier to change the magnitude of the unit. Below is a table of unit prefixes and their effect on the magnitude of the unit.
| Prefix: | Symbol: | Magnitude: | Prefix: | Symbol: | Magnitude: | |
|---|---|---|---|---|---|---|
| Yotta- | Y | 1024 | deci- | d | 10-1 | |
| Zetta- | Z | 1021 | centi- | c | 10-2 | |
| Exa- | E | 1018 | milli- | m | 10-3 | |
| Peta- | P | 1015 | micro- | μ (mu) | 10-6 | |
| Tera- | T | 1012 | nano- | n | 10-9 | |
| Giga- | G | 109 | pico- | p | 10-12 | |
| Mega- | M | 106 | femto- | f | 10-15 | |
| kilo- | k | 103 | atto- | a | 10-18 | |
| hecto- | h | 102 | zepto- | z | 10-21 | |
| deka- | da | 10 | yocto- | y | 10-24 |
For example, 1000 meters = 10 hectometers = 1 km = 1000000 mm = 1 x 109 micrometers.
Significant Figures
It is important to make a distinction between the words, "accuracy", and, "precision".
Accuracy - The ability of a measurement to match the actual value of the quantity being measured.
Precision - The ability of a measurement to be consistently reproduced.
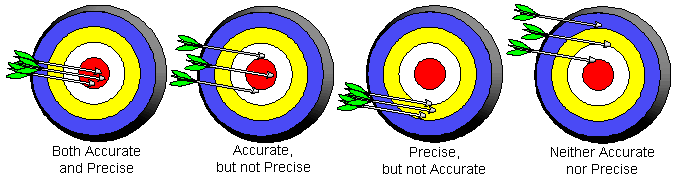
A measurement can never be more precise than its least precise digit. The precision of a measurement depends on the instrument used.
For example, using a ruler marked off in millimeters will yield a much more precise measurement than a stick only marked in meters.
If you are asked to measure then length of a pencil using a ruler marked in millimeters, you could say the pencil is 82 mm long.
But if you look very closely, one can see that the tip of the pencil extends slightly further, but since the ruler is not marked in small enough increments to tell exactly the length, we can make an estimate as to where the next line would be. Looking very closely, we can see the tip is half way between the 82 and 83 mm making, thus we can estimate the pencils length as 82.5 mm.
One is only allowed to estimate one digit past the smallest digit the instrument can measure. This estimated digit introduces a degree of inaccuracy into the measurement. The previous measurement taken with the ruler has an accuracy of + .1 mm.
When performing calculations with measurements, it is important to take Significant Figures into account in order to maintain the correct precision (or imprecision) in the answer.
Significant Figure Rules
Determining Significant Digits:
-
Non zero digits - non-zero numbers are significant
-
Zeros - There are three types:
a) Leading zeros are zeros that precede all non-zero digits. These zeros are not significant figures.
b) Captive zeros are zeros between sig. figs., usually non-zero digits. These zeros are significant figures.
c) Trailing zeros are zeros at the right end of the number. They are sig. figs. only if the number contains a decimal point. -
Exact numbers are numbers that are derived by counting or by definition (for example: π or the rest mass of an electron). These numbers have infinite number of sig. figs.
Performing Calculations:
Addition/Subtraction -The final answer should have the same number of digits to the right of the decimal as the measurement with the smallest number of digits to the right of the decimal place.
Multiplication/Division - The final answer should have the same number of significant figures as the measurement having the smallest number of significant figures.
Rounding:
-
Round Down
-Whenever the digit following the last significant figure is less than 5 (i.e. 0, 1, 2, 3, 4).
-If the last significant figure is an even number and the next digit is a 5, with no other non-zero digits. -
Round Up
-Whenever the digit following the last significant digit is greater than 5 (i.e. 6, 7, 8, 9).
-If the digit following the last significant digit is a 5 followed by a non-zero digit.
-If the last significant digit is an odd number and the next digit is a 5, with no other non-zero digits.
Last updated: 05/20/2019